Im Anfangsunterricht stellt das Erlernen von Mengenerfassungsstrategien einen fundamentalen Schritt für Schülerinnen und Schüler dar, um ein tiefes Verständnis für Zahlen und Mathematik zu entwickeln. Dabei wird zwischen zwei grundlegenden Ansätzen unterschieden: zählenden und nicht-zählenden Strategien. Beide Strategien sind von entscheidender Bedeutung, um Kindern ein umfassendes Zahlenverständnis zu vermitteln, und sie ergänzen sich gegenseitig in der mathematischen Frühbildung.
Zählende Strategie
Bereits vor der Einschulung sammeln die Kinder im Kindergarten und im Alltag erste mathematische Erfahrungen. In der Kooperation zwischen Kindergarten und Schule treffe ich jedes Jahr auf viele – sehr stolze – zukünftige Erstklässler. Das erste, was die Kinder mir erzählen, wenn sie hören, dass ich „von der Schule komme”, ist, wie weit sie bereits zählen können. Die „Zählende Strategie” umfasst jedoch mehr als das sichere Aufsagen der Zahlwortreihe.
Zählende Strategien basieren auf der Erfassung von Mengen durch Abzählen von Einzelobjekten. Diese Methode stellt eine der ersten mathematischen Fähigkeiten dar, die Kinder erlernen. Das sequenzielle Zählen vermittelt Kindern ein konkretes Verständnis dafür, dass jede Zahl einem spezifischen Mengenwert entspricht. Dies kann beispielsweise durch das Legen von Steinen in einer Reihe und das Zählen jedes Steins einzeln demonstriert werden, um die Gesamtzahl zu ermitteln. Zählende Strategien erweisen sich als nützlich, um die Grundlagen des Zahlbegriffs zu festigen. Sie unterstützen Kinder dabei, zu verstehen, dass die letzte ausgesprochene Zahl die Anzahl aller gezählten Objekte angibt. Diese Einsicht ist von entscheidender Bedeutung für das Verständnis weiterführender mathematischer Konzepte wie Addition und Subtraktion.
Kardinales Zahlverständnis
Das kardinale Zahlverständnis bezieht sich darauf, wie viele Objekte eine Zahl darstellt. Nehmen wir zum Beispiel die Zahl „drei”. Sie steht für drei Objekte. Dieses Verständnis ist wichtig, um Addition, Subtraktion und weitere Rechenarten zu lernen. Es hilft dabei, Mengen und deren Veränderung zu verstehen.
Im Unterricht kann das kardinale Zahlverständnis durch viele verschiedene Aktivitäten gefördert werden. Zum Beispiel kann man Objekte zählen, Gruppen von Objekten zusammenfügen und trennen oder Zählhilfen wie Abakus oder Zählsteine verwenden. Lehrkräfte können Kinder anleiten, Objekte zu zählen und dabei laut die Zahlen zu benennen. So wird die Verbindung zwischen der numerischen Bezeichnung und der physischen Quantität verstärkt.
In den Bildungsplänen lässt sich das kardinale Zahlverständnis in den folgenden Bereich finden:
Zahlen und Mengen erkennen und benennen: Die Kinder lernen, Zahlen bis zu einer bestimmten Größe (oft bis 20) zu erkennen und die entsprechende Anzahl von Objekten einer Zahl zuzuordnen.
Zählen und Zuordnen: Die Kinder zählen Objekte und können die gezählte Anzahl einer Zahl zuordnen.
Vergleichen und Ordnen von Mengen: Die Kinder vergleichen zählend Mengen, indem sie bestimmen, welche Menge größer oder kleiner ist, oder Mengen nach Größe ordnen.
Anwenden von Zahlen in Alltagssituationen: Kinder sollen lernen, Zahlen und Mengen in alltäglichen Kontexten zu verwenden, beispielsweise beim Abzählen von Gegenständen, beim Verteilen von Snacks oder beim Bestimmen der Anzahl von Personen in einer Gruppe.
Erkennen von Mustern und Strukturen: Das Erkennen und Nutzen von Mustern, wie sie zum Beispiel in Zahlenreihen oder bei der Anordnung von Objekten auftreten, unterstützt das Verständnis von Zahlen und Mengen.
Einfache Addition und Subtraktion: Das Verständnis von Addition und Subtraktion als Hinzufügen zu oder Wegnehmen von einer Menge fördert das kardinale Verständnis.
Das ordinale Zahlverständnis bezieht sich darauf, wo man in einer Reihe steht. Es geht darum zu verstehen, dass „der dritte” in einer Reihe auf die Position oder den Rang verweist. Dieses Verständnis ist wichtig für die Entwicklung von Fähigkeiten wie das Vergleichen von Mengen, das Ordnen von Zahlen und das Verstehen von Reihenfolgen.
Im Klassenzimmer kann das ordinale Zahlverständnis durch Spiele und Aktivitäten gefördert werden, bei denen Kinder Objekte in einer bestimmten Reihenfolge anordnen müssen. Zum Beispiel beim Anstellen nach Größe oder beim Ordnen von Zahlenkarten von der kleinsten zur größten Zahl.
ordinares Zahlverständnis
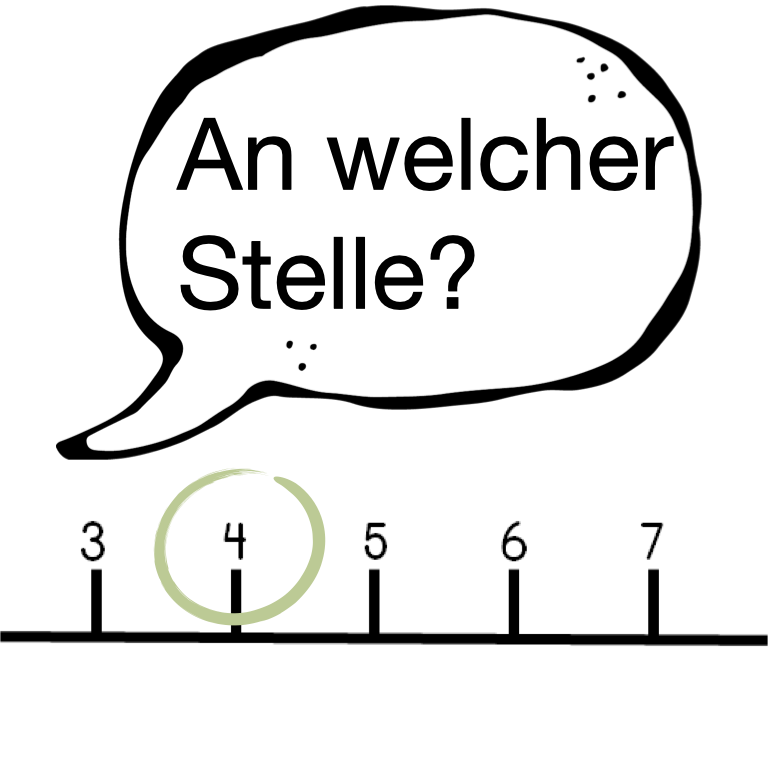
Auch Geschichten und Szenarien, in denen Kinder gefragt werden, wer Erster, Zweiter oder Dritter in einem Wettbewerb war, helfen dabei, das ordinale Verständnis zu vertiefen.
Reihenfolge und Position verstehen: Die Kinder lernen, die Position von Objekten innerhalb einer Sequenz zu erkennen und zu benennen. Sie sollen verstehen, dass beispielsweise das dritte Tier in einer Reihe das Tier ist, das nach zwei anderen Tieren kommt.
Zahlen in einer Reihe ordnen: Die Kinder ordnen Zahlen in aufsteigender oder absteigender Reihenfolge. Diese Aktivität hilft ihnen, das Konzept der Reihenfolge zu verstehen und zu verinnerlichen.
Vergleichen von Positionen: Die Kinder lernen, Objekte oder Zahlen basierend auf ihrer Position zu vergleichen, indem sie Begriffe wie “vor”, “nach”, “zwischen”, “erster”, “letzter” etc. verwenden.
Anwenden ordinaler Konzepte in Alltagssituationen: Die Kinder nutzen ordinale Begriffe, um alltägliche Situationen zu beschreiben, wie z.B. die Bestimmung, wer der zweite in der Schlange ist oder welches Kind als drittes an der Reihe ist.
Spielerische Aktivitäten: Spiele, bei denen Kinder Objekte nach Anweisungen sortieren müssen (z.B. “Stelle das rote Auto an die dritte Stelle”), fördern das Verständnis für ordinale Zahlen.
Nicht-zählende Strategie
Die Fähigkeit, die Anzahl von Objekten in einer Gruppe zu bestimmen, ohne diese einzeln zählen zu müssen, wird als „Mengen erfassen” bezeichnet. Diese grundlegende mathematische Fähigkeit wird im Rahmen des Anfangsunterrichts in Mathematik entwickelt. Kinder lernen, kleine Mengen auf einen Blick zu erkennen und zu benennen. Sie sind beispielsweise in der Lage, sofort zu erkennen und zu verstehen, dass drei Äpfel auf einem Tisch liegen, ohne jeden Apfel einzeln zu zählen. Die Entwicklung dieser Fähigkeit stellt eine wesentliche Grundlage für das Verständnis von Zahlen und Mengen dar und bildet somit eine Vorstufe zum zählenden Rechnen.
"quasi-simultan"
Die quasi-simultane Mengenerfassung ermöglicht die Erfassung von Mengen bis zu einer bestimmten Größe (meist bis zu vier oder fünf Objekten) „auf einen Blick“.
Die quasi-simultane Mengenerfassung bezeichnet das schnelle, genaue und sichere Erkennen von Anzahlen, ohne dass die Objekte einzeln gezählt werden müssen.
Die Erfassung erfolg “quasi-simultan”, da Mengen größer als vier oder fünf nicht auf einmal erfasst werden können. Durch Bündelung können größere Mengen “quasi-simultan” erfasst werden.
Zählen und Erfassen
Im Gegensatz zum zählenden Erfassen von Mengen, bei dem jedes Objekt einzeln gezählt wird, ermöglicht die quasi-simultane Mengenerfassung eine sofortige Identifikation der Menge. Dies ist schneller und effizienter, besonders bei kleineren Mengen.
Bei größeren Mengen, die über die Kapazität des simultanen Erfassens hinausgehen, neigen Menschen dazu, entweder zu schätzen oder die Objekte in kleinere Gruppen zu unterteilen und diese dann zu zählen (Bündeln).
Grundlagen legen
In der Schuleingangsstufe ist die Förderung der quasi-simultanen Mengenerfassung von besonderer Bedeutung, da sie die Basis für weiterführende mathematische Fähigkeiten bildet.
Kinder, die über eine hohe Fähigkeit zur quasi-simultanen Mengenerfassung verfügen, sind in der Lage, mathematische Probleme schneller und effektiver zu lösen. Dies ist darauf zurückzuführen, dass sie weniger Zeit für das Zählen benötigen und ein besseres Verständnis für Zahlen und Mengen entwickeln.
Förderung
Wir können die Entwicklung dieser Fähigkeit unterstützen, indem wir Aktivitäten und Spiele einsetzen, die Kinder herausfordern, Mengen schnell zu erkennen.
Dazu zählen beispielsweise Spiele mit Würfeln, bei denen die Punkte auf den Würfelflächen quasi-simultan erfasst werden müssen oder Flashcards mit verschiedenen Anzahlen von Symbolen, die kurz gezeigt werden.